基于贝叶斯推断应用原理的过滤垃圾邮件研究

随着电子邮件的应用与普及，垃圾邮件的泛滥也越来越多地受到人们的关注。而目前正确识别垃圾邮件的技术难度非常大。传统的垃圾邮件过滤方法，主要有"关键词法"和"校验码法"等。前者的过滤依据是特定的词语；后者则是计算邮件文本的校验码，再与已知的垃圾邮件进行对比。它们的识别效果都不理想，而且很容易规避。

所以今天我要在马海祥博客上跟大家分享的就是基于贝叶斯的垃圾邮件过滤器的原理及其关键技术进行的垃圾邮件过滤。针对贝叶斯模型对分类信息过度简化和准确率低等缺点，通过引入分级的最小风险算法和对多项式和多重贝努利估计模型进行混合的方法分别对贝叶斯过滤器进行了改进，并进行了实验。实验结果表明，改进后的贝叶斯过滤器具有了更好过滤效果。

一、贝叶斯推断是什么？

贝叶斯推断（Bayesian inference）是一种应用于不确定性条件下的决策的统计方法，用来估计统计量的某种性质。贝叶斯推断的显著特征是，为了得到一个统计结论能够利用先验信息和样本信息。

1、贝叶斯推断产生背景

贝叶斯推断是贝叶斯定理（Bayes' theorem）的应用。英国数学家托马斯·贝叶斯（Thomas Bayes）在1763年发表的一篇论文中，首先提出了这个定理。

贝叶斯推断与其他统计学推断方法截然不同。它建立在主观判断的基础上，也就是说，你可以不需要客观证据，先估计一个值，然后根据实际结果不断修正。正是因为它的主观性太强，曾经遭到许多统计学家的诟病。

另外，贝叶斯推断需要大量的计算，因此历史上很长一段时间，无法得到广泛应用。只有计算机诞生以后，它才获得真正的重视。人们发现，许多统计量是无法事先进行客观判断的，而互联网时代出现的大型数据集，再加上高速运算能力，为验证这些统计量提供了方便，也为应用贝叶斯推断创造了条件，它的威力正在日益显现。

2、贝叶斯推断的主要术语

客观概率(OBJECTIVE PROBABILITY)：对重复出现的现象给出的一种概率解释。

参数(PARAMETER)：一个概率分布的数字特征。概率(PROBABILITY)：把一个实数与教学集合中的一个元素联系起来的数学函数。

统计量(STATISTIC)：通过样本数据计算得到的一次试验的数值结果。

主观概率(SUBJECTIVE PROBABILITY)：基于个人对不确定事件结果的信念度而推断出的概率。

二、贝叶斯定理

要理解贝叶斯推断，必须先理解贝叶斯定理。后者实际上就是计算“条件概率”的公式。

所谓"条件概率"（Conditional probability），就是指在事件B发生的情况下，事件A发生的概率，用P(A|B)来表示：

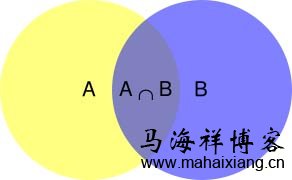
根据上图所示，可以很清楚地看到在事件B发生的情况下，事件A发生的概率就是P(A∩B)除以P(B)：

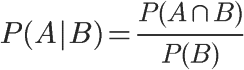
因此：

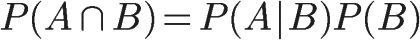
同理可得：

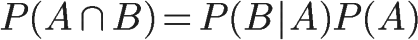
所以：

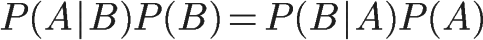
即：

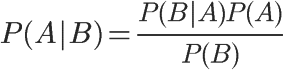
这就是条件概率的计算公式。

三、全概率公式

由于后面要用到，所以除了条件概率以外，这里还要推导全概率公式。

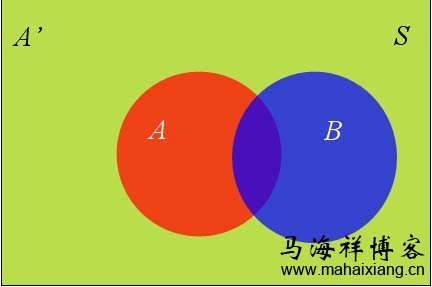
假定样本空间S，是两个事件A与A'的和：

上图中，红色部分是事件A，绿色部分是事件A'，它们共同构成了样本空间S。

在这种情况下，事件B可以划分成两个部分。

即：

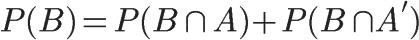
在上一节的推导当中，我们已知：

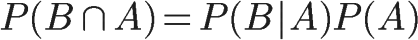
所以：

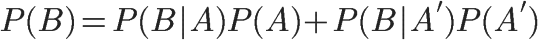
这就是全概率公式。它的含义是，如果A和A'构成样本空间的一个划分，那么事件B的概率，就等于A和A'的概率分别乘以B对这两个事件的条件概率之和。

将这个公式代入上一节的条件概率公式，就得到了条件概率的另一种写法：

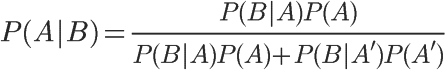
四、贝叶斯推断的含义

对条件概率公式进行变形，可以得到如下形式：

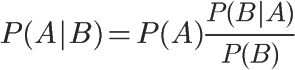
我们把P(A)称为"先验概率"（Prior probability），即在B事件发生之前，马海祥先对A事件概率的一个判断。

P(A|B)称为"后验概率"（Posterior probability），即在B事件发生之后，马海祥再对A事件概率的重新评估。

P(B|A)/P(B)称为"可能性函数"（Likelyhood），这是一个调整因子，使得预估概率更接近真实概率。

所以，条件概率可以理解成下面的式子：

后验概率＝先验概率ｘ调整因子

这就是贝叶斯推断的含义。我们先预估一个"先验概率"，然后加入实验结果，看这个实验到底是增强还是削弱了"先验概率"，由此得到更接近事实的"后验概率"。

在这里，如果"可能性函数"P(B|A)/P(B)>1，意味着"先验概率"被增强，事件A的发生的可能性变大；如果"可能性函数"=1，意味着B事件无助于判断事件A的可能性；如果"可能性函数"<1，意味着"先验概率"被削弱，事件A的可能性变小。

五、通过事例来理解贝叶斯推断

为了加深对贝叶斯推断的理解，我们看两个例子。

例子1：水果糖问题

两个一模一样的碗，一号碗有30颗水果糖和10颗巧克力糖，二号碗有水果糖和巧克力糖各20颗。现在随机选择一个碗，从中摸出一颗糖，发现是水果糖。请问这颗水果糖来自一号碗的概率有多大？

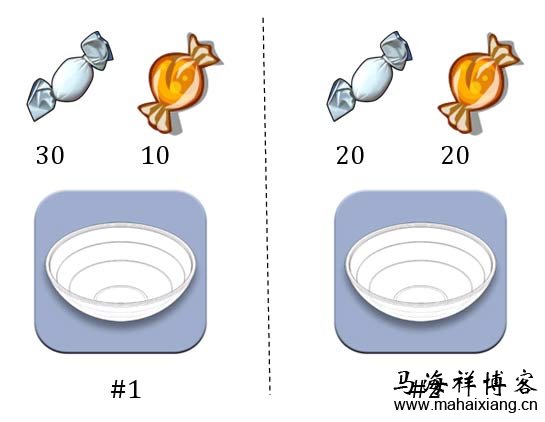
我们假定，H1表示一号碗，H2表示二号碗。由于这两个碗是一样的，所以P(H1)=P(H2)，也就是说，在取出水果糖之前，这两个碗被选中的概率相同。因此，P(H1)=0.5，我们把这个概率就叫做"先验概率"，即没有做实验之前，来自一号碗的概率是0.5。

再假定，E表示水果糖，所以问题就变成了在已知E的情况下，来自一号碗的概率有多大，即求P(H1|E)。我们把这个概率叫做"后验概率"，即在E事件发生之后，对P(H1)的修正。

根据条件概率公式，得到：

已知，P(H1)等于0.5，P(E|H1)为一号碗中取出水果糖的概率，等于0.75，那么求出P(E)就可以得到答案。根据全概率公式：

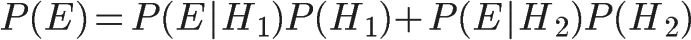
所以：

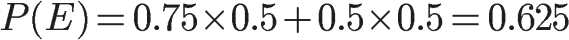
将数字代入原方程，得到：

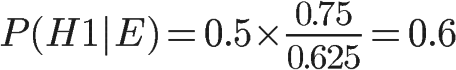
这表明，来自一号碗的概率是0.6。也就是说，取出水果糖之后，H1事件的可能性得到了增强。

例子2：假阳性问题

第二个例子是一个医学的常见问题，与现实生活关系紧密。

已知某种疾病的发病率是0.001，即1000人中会有1个人得病。现有一种试剂可以检验患者是否得病，它的准确率是0.99，即在患者确实得病的情况下，它有99%的可能呈现阳性。它的误报率是5%，即在患者没有得病的情况下，它有5%的可能呈现阳性。现有一个病人的检验结果为阳性，请问他确实得病的可能性有多大？

假定A事件表示得病，那么P(A)为0.001。这就是"先验概率"，即没有做试验之前，我们预计的发病率。再假定B事件表示阳性，那么要计算的就是P(A|B)。这就是"后验概率"，即做了试验以后，对发病率的估计。

根据条件概率公式：

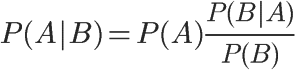
用全概率公式改写分母：

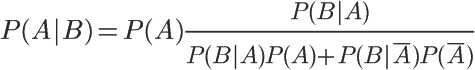
将数字代入：

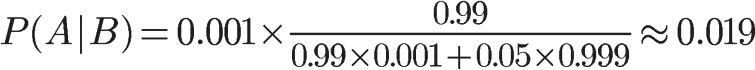
我们得到了一个惊人的结果，P(A|B)约等于0.019。也就是说，即使检验呈现阳性，病人得病的概率，也只是从0.1%增加到了2%左右。这就是所谓的"假阳性"，即阳性结果完全不足以说明病人得病。

为什么会这样？为什么这种检验的准确率高达99%，但是可信度却不到2%？答案是与它的误报率太高有关。

有兴趣的朋友，还可以利用马海祥博客上面所阐述的公式算一下"假阴性"问题，即检验结果为阴性，但是病人确实得病的概率有多大。然后问自己，"假阳性"和"假阴性"，哪一个才是医学检验的主要风险？

六、什么是贝叶斯过滤器？

贝叶斯过滤器（Bayesian filter）通过使用贝叶斯逻辑（或称贝叶斯分析法），对邮件的标题和内容进行分析，从而判断邮件是否是垃圾邮件。

正确识别垃圾邮件的技术难度非常大。传统的垃圾邮件过滤方法，主要有"关键词法"和"校验码法"等。前者的过滤依据是特定的词语；后者则是计算邮件文本的校验码，再与已知的垃圾邮件进行对比。它们的识别效果都不理想，而且很容易规避。

2002年，Paul Graham提出使用"贝叶斯推断"过滤垃圾邮件。他说，这样做的效果，好得不可思议。当时声称：1000封垃圾邮件可以过滤掉995封，且没有一个误判。

另外，这种过滤器还具有自我学习的功能，会根据新收到的邮件，不断调整。收到的垃圾邮件越多，它的准确率就越高。

马海祥认为贝叶斯过滤器也不是万能的。毕竟垃圾邮件包含有特定的文字，贝叶斯过滤器需要进行一段时间的学习，才能对垃圾邮件做出有效的拦截。贝叶斯过滤器会根据概率把邮件分类，比如："信任邮件"、"可疑邮件"等等。分类的类别可以由用户自己定义。

七、建立历史资料库

贝叶斯过滤器是一种统计学过滤器，建立在已有的统计结果之上。所以，我们必须预先提供两组已经识别好的邮件，一组是正常邮件，另一组是垃圾邮件。

我们用这两组邮件，对过滤器进行"训练"。这两组邮件的规模越大，训练效果就越好。Paul Graham使用的邮件规模，是正常邮件和垃圾邮件各4000封。

"训练"过程很简单。首先，解析所有邮件，提取每一个词。然后，计算每个词语在正常邮件和垃圾邮件中的出现频率。比如，我们假定"sex"这个词，在4000封垃圾邮件中，有200封包含这个词，那么它的出现频率就是5%；而在4000封正常邮件中，只有2封包含这个词，那么出现频率就是0.05%。（【注释】如果某个词只出现在垃圾邮件中，Paul Graham就假定，它在正常邮件的出现频率是1%，反之亦然。这样做是为了避免概率为0。随着邮件数量的增加，计算结果会自动调整。）

有了这个初步的统计结果，过滤器就可以投入使用了。

八、贝叶斯过滤器的使用过程

现在，假如我们收到了一封新邮件。在未经统计分析之前，我们假定它是垃圾邮件的概率为50%。（【注释】有研究表明，用户收到的电子邮件中，80%是垃圾邮件。但是，这里仍然假定垃圾邮件的"先验概率"为50%。）

我们用S表示垃圾邮件（spam），H表示正常邮件（healthy）。因此，P(S)和P(H)的先验概率，都是50%。

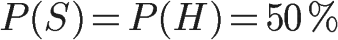
然后，对这封邮件进行解析，发现其中包含了sex这个词，请问这封邮件属于垃圾邮件的概率有多高？
我们用W表示"sex"这个词，那么问题就变成了如何计算P(S|W)的值，即在某个词语（W）已经存在的条件下，垃圾邮件（S）的概率有多大。

根据条件概率公式，马上可以写出：

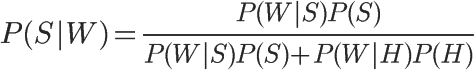
公式中，P(W|S)和P(W|H)的含义是，这个词语在垃圾邮件和正常邮件中，分别出现的概率。这两个值可以从历史资料库中得到，对sex这个词来说，上文假定它们分别等于5%和0.05%。另外，P(S)和P(H)的值，前面说过都等于50%。所以，马上可以计算P(S|W)的值：

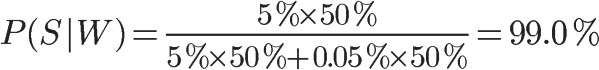
因此，这封新邮件是垃圾邮件的概率等于99%。这说明，sex这个词的推断能力很强，将50%的"先验概率"一下子提高到了99%的"后验概率"。

九、联合概率的计算

做完上面一步，请问我们能否得出结论，这封新邮件就是垃圾邮件？

回答是不能。因为一封邮件包含很多词语，一些词语（比如sex）说这是垃圾邮件，另一些说这不是。你怎么知道以哪个词为准？

Paul Graham的做法是，选出这封信中P(S|W)最高的15个词，计算它们的联合概率。（【注释】如果有的词是第一次出现，无法计算P(S|W)，Paul Graham就假定这个值等于0.4。因为垃圾邮件用的往往都是某些固定的词语，所以如果你从来没见过某个词，它多半是一个正常的词。）

所谓联合概率，就是指在多个事件发生的情况下，另一个事件发生概率有多大。比如，已知W1和W2是两个不同的词语，它们都出现在某封电子邮件之中，那么这封邮件是垃圾邮件的概率，就是联合概率。

在已知W1和W2的情况下，无非就是两种结果：垃圾邮件（事件E1）或正常邮件（事件E2）。

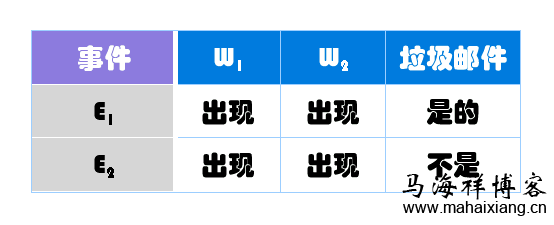
其中，W1、W2和垃圾邮件的概率分别如下：

如果假定所有事件都是独立事件（【注释】严格地说，这个假定不成立，但是这里可以忽略），那么就可以计算P(E1)和P(E2)：

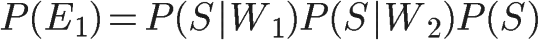
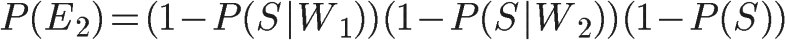
又由于在W1和W2已经发生的情况下，垃圾邮件的概率等于下面的式子：

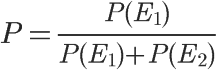
即：

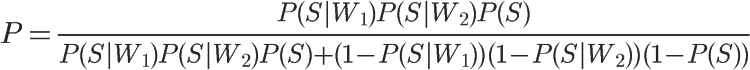
将P(S)等于0.5代入，得到：

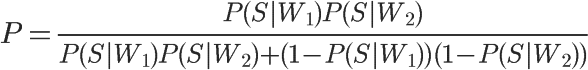
将P(S|W1)记为P1，P(S|W2)记为P2，公式就变成：

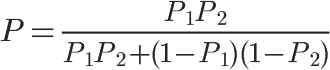
这就是联合概率的计算公式。如果你不是很理解，点击这里查看更多的解释。

十、最终的概率计算公式

将上面的公式扩展到15个词的情况，就得到了最终的概率计算公式：

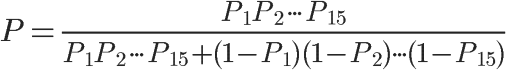
一封邮件是不是垃圾邮件，就用这个式子进行计算。这时我们还需要一个用于比较的门槛值。Paul Graham的门槛值是0.9，概率大于0.9，表示15个词联合认定，这封邮件有90%以上的可能属于垃圾邮件；概率小于0.9，就表示是正常邮件。有了这个公式以后，一封正常的信件即使出现sex这个词，也不会被认定为垃圾邮件了。

本文发布于马海祥博客文章，如想转载，请注明原文网址摘自于https://www.mahaixiang.cn/internet/312.html，注明出处；否则，禁止转载；谢谢配合！